DS 5100: Programming for Data Science - 35 NB: Introducing Pandas II

Set Up

import numpy as np
import pandas as pd
import seaborn as sns
iris = sns.load_dataset('iris')

iris.head(2)

	sepal_length	sepal_width	petal_length	petal_width	species
0	5.1	3.5	1.4	0.2	setosa
1	4.9	3.0	1.4	0.2	setosa

import sys
sys.getsizeof(iris)

Apply Lambda Functions with `.apply()`

Apply a transformation to each record. Uses a lambda function.

The apply() method should be used after you have established that you can’t use a vectorized function.

iris['sepal_len_sq'] = iris.sepal_length.apply(lambda x: x**2)
iris.head(5)

	sepal_length	sepal_width	petal_length	petal_width	species	sepal_len_sq
0	5.1	3.5	1.4	0.2	setosa	26.01
1	4.9	3.0	1.4	0.2	setosa	24.01
2	4.7	3.2	1.3	0.2	setosa	22.09
3	4.6	3.1	1.5	0.2	setosa	21.16
4	5.0	3.6	1.4	0.2	setosa	25.00

Transformation involving multiple columns. Uses axis=1 to access columns.
Compute average of sepal_length, sepal_width:

iris['sepal_len_wid_avg'] = iris[['sepal_length','sepal_width']]\
    .apply(lambda x: (x.sepal_length + x.sepal_width) / 2, axis=1)
iris.head()

	sepal_length	sepal_width	petal_length	petal_width	species	sepal_len_sq	sepal_len_wid_avg
0	5.1	3.5	1.4	0.2	setosa	26.01	4.30
1	4.9	3.0	1.4	0.2	setosa	24.01	3.95
2	4.7	3.2	1.3	0.2	setosa	22.09	3.95
3	4.6	3.1	1.5	0.2	setosa	21.16	3.85
4	5.0	3.6	1.4	0.2	setosa	25.00	4.30

Vectorized Version

%time iris.sepal_length**2

CPU times: user 306 µs, sys: 18 µs, total: 324 µs
Wall time: 343 µs

0      26.01
1      24.01
2      22.09
3      21.16
4      25.00
       ...  
145    44.89
146    39.69
147    42.25
148    38.44
149    34.81
Name: sepal_length, Length: 150, dtype: float64

Compare to .apply()

%time iris.sepal_length.apply(lambda x: x**2)

CPU times: user 830 µs, sys: 200 µs, total: 1.03 ms
Wall time: 1.23 ms

0      26.01
1      24.01
2      22.09
3      21.16
4      25.00
       ...  
145    44.89
146    39.69
147    42.25
148    38.44
149    34.81
Name: sepal_length, Length: 150, dtype: float64

Aggregation

Involves one or more of:

splitting the data into groups
applying a function to each group
combining results

`.groupby()`

Compute mean of each column, grouped (separately) by species

iris.groupby("species").mean()

	sepal_length	sepal_width	petal_length	petal_width	sepal_len_sq	sepal_len_wid_avg
species
setosa	5.006	3.428	1.462	0.246	25.1818	4.217
versicolor	5.936	2.770	4.260	1.326	35.4972	4.353
virginica	6.588	2.974	5.552	2.026	43.7980	4.781

`pd.pivot_table()`

Apply a function aggfunc to selected values grouped by columns

Details

Compute mean sepal length for each species:

pd.pivot_table(iris, values="sepal_length", columns=["species"], aggfunc = np.mean)

species	setosa	versicolor	virginica
sepal_length	5.006	5.936	6.588

Stacking and Unstacking

Similar to pivoting, but requires – and takes advantage of – indexes.

`.unstack()`

Details

Let’s look at what unstack() does with a dataset from Seaborn’s collection.

attention = sns.load_dataset('attention')

attention.sample(10)

	Unnamed: 0	subject	attention	solutions	score
5	5	6	divided	1	5.0
40	40	1	divided	3	7.0
11	11	12	focused	1	8.0
12	12	13	focused	1	6.0
24	24	5	divided	2	5.0
9	9	10	divided	1	6.0
0	0	1	divided	1	2.0
37	37	18	focused	2	8.0
7	7	8	divided	1	5.0
22	22	3	divided	2	5.0

This dataframe appears to record the results of an experiment on human attention.

Each row is a trial or observation in that experiment.

An analysis of the columns in this dataframe show that score is a measured outcome, subjects are probably individuals in a comparative study where two groups, those with attention divided and those with attention focused, are subject to three different solutions applied to the performance of some task. Unnamed: 0 is just the row number as index.

The purpose of the test performed in each trial seems to be see which solutions are best at overcoming divied attention in the performance of those tasks.

Let’s restructure our data to reflect these assumptions.

attention1 = attention.set_index(['attention','solutions','subject']).sort_index().drop('Unnamed: 0', axis=1)

attention1.head(20)

			score
attention	solutions	subject
divided	1	1	2.0
		2	3.0
		3	3.0
		4	5.0
		5	4.0
		6	5.0
		7	5.0
		8	5.0
		9	2.0
		10	6.0
	2	1	4.0
		2	4.0
		3	5.0
		4	7.0
		5	5.0
		6	5.0
		7	4.5
		8	7.0
		9	3.0
		10	5.0

We can use .unstack() to provide a nice, synoptic view of these data.

attention2 = attention1.unstack()
attention2.fillna('')

		score
	subject	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20
attention	solutions
divided	1	2.0	3.0	3.0	5.0	4.0	5.0	5.0	5.0	2.0	6.0
	2	4.0	4.0	5.0	7.0	5.0	5.0	4.5	7.0	3.0	5.0
	3	7.0	5.0	6.0	5.0	8.0	6.0	6.0	8.0	7.0	6.0
focused	1											6.0	8.0	6.0	8.0	8.0	6.0	7.0	7.0	5.0	6.0
	2											5.0	9.0	5.0	8.0	8.0	8.0	7.0	8.0	6.0	6.0
	3											6.0	8.0	9.0	7.0	7.0	7.0	6.0	6.0	6.0	5.0

We can see clearly the data from two groups by attention, each consisting of 10 subjects, each employing three solutions.

By unstacking again, we can get a sense of which solution worked best.

attention2.mean(1).unstack().T.style.background_gradient(axis=None)

attention	divided	focused
solutions
1	4.000000	6.700000
2	4.950000	7.000000
3	6.400000	6.700000

It appears the solution 3 performed well.

`.stack()`

Stack is the opposite of .unstack(), of course. It will project a column name series into the values of a single column.

Details

Let look at this with the taxis database.

taxis = sns.load_dataset('taxis')

taxis.head()

	pickup	dropoff	passengers	distance	fare	tip	total	color	payment	pickup_zone	dropoff_zone	pickup_borough	dropoff_borough
0	2019-03-23 20:21:09	2019-03-23 20:27:24	1	1.60	7.0	2.15	12.95	yellow	credit card	Lenox Hill West	UN/Turtle Bay South	Manhattan	Manhattan
1	2019-03-04 16:11:55	2019-03-04 16:19:00	1	0.79	5.0	0.00	9.30	yellow	cash	Upper West Side South	Upper West Side South	Manhattan	Manhattan
2	2019-03-27 17:53:01	2019-03-27 18:00:25	1	1.37	7.5	2.36	14.16	yellow	credit card	Alphabet City	West Village	Manhattan	Manhattan
3	2019-03-10 01:23:59	2019-03-10 01:49:51	1	7.70	27.0	6.15	36.95	yellow	credit card	Hudson Sq	Yorkville West	Manhattan	Manhattan
4	2019-03-30 13:27:42	2019-03-30 13:37:14	3	2.16	9.0	1.10	13.40	yellow	credit card	Midtown East	Yorkville West	Manhattan	Manhattan

taxis1 = taxis.set_index(['pickup','dropoff']).sort_index().stack().to_frame('val')
taxis1.index.names = ['pickup','dropoff','field']

taxis1.sample(10)

			val
pickup	dropoff	field
2019-03-23 13:13:20	2019-03-23 13:15:13	dropoff_zone	Hudson Sq
2019-03-21 01:30:10	2019-03-21 01:50:15	tolls	0.0
2019-03-04 14:13:31	2019-03-04 14:24:15	tolls	0.0
2019-03-06 21:00:00	2019-03-06 21:04:45	passengers	1
2019-03-08 21:43:33	2019-03-08 21:45:48	tolls	0.0
2019-03-07 14:27:58	2019-03-07 14:45:49	pickup_borough	Queens
2019-03-14 15:11:21	2019-03-14 15:21:02	dropoff_zone	Upper West Side North
2019-03-14 16:49:58	2019-03-14 17:07:29	fare	14.5
2019-03-13 16:16:05	2019-03-13 16:28:11	dropoff_borough	Manhattan
2019-03-10 16:13:48	2019-03-10 16:17:53	total	7.8

taxis1.loc['2019-02-28 23:29:03']

		val
dropoff	field
2019-02-28 23:32:35	passengers	1
	distance	0.9
	fare	5.0
	tip	0.0
	tolls	0.0
	total	6.3
	color	green
	payment	cash
	pickup_zone	Old Astoria
	dropoff_zone	Long Island City/Queens Plaza
	pickup_borough	Queens
	dropoff_borough	Queens

Combining DataFrames

`pd.concat()`

Concatenate pandas objects along an axis.

Details

Create two dfs and vertically stack them

df1 = pd.DataFrame(np.random.randn(3, 4))
df2 = pd.DataFrame(np.random.randn(3, 4))

df1

	0	1	2	3
0	-0.334874	-1.179623	-0.369825	0.748533
1	-0.376463	-1.813195	-0.342195	-0.732275
2	0.184883	-0.745494	0.503854	0.497544

df2

	0	1	2	3
0	1.411402	-0.543350	-0.020294	0.789886
1	0.786837	0.960382	-1.093336	0.551457
2	0.582368	1.606100	1.715443	-0.481616

Concat rows

df3 = pd.concat([df1, df2], axis=0)

df3

	0	1	2	3
0	-0.334874	-1.179623	-0.369825	0.748533
1	-0.376463	-1.813195	-0.342195	-0.732275
2	0.184883	-0.745494	0.503854	0.497544
0	1.411402	-0.543350	-0.020294	0.789886
1	0.786837	0.960382	-1.093336	0.551457
2	0.582368	1.606100	1.715443	-0.481616

Concat columns

This assumes that the indexes represent IDs of specific things or events.

df4 = pd.concat([df1, df2], axis=1, keys=['foo', 'bar'])

df4

	foo				bar
	0	1	2	3	0	1	2	3
0	-0.334874	-1.179623	-0.369825	0.748533	1.411402	-0.543350	-0.020294	0.789886
1	-0.376463	-1.813195	-0.342195	-0.732275	0.786837	0.960382	-1.093336	0.551457
2	0.184883	-0.745494	0.503854	0.497544	0.582368	1.606100	1.715443	-0.481616

df4.foo

	0	1	2	3
0	-0.334874	-1.179623	-0.369825	0.748533
1	-0.376463	-1.813195	-0.342195	-0.732275
2	0.184883	-0.745494	0.503854	0.497544

`.merge()`

SQL-style joining of tables (DataFrames) – although Pandas has a .join() method, too.

Important parameters include:

how : type of merge {‘left’, ‘right’, ‘outer’, ‘inner’, ‘cross’}, default ‘inner’
on : names to join on

Details

Create two tables, left and right. Then right join them on key.
Right join means include all records from table on right.
The key is used for matching up the records.

left = pd.DataFrame({"key": ["jamie", "bill"], "lval": [15, 22]})
right = pd.DataFrame({"key": ["jamie", "bill", "asher"], "rval": [4, 5, 8]})
merged = pd.merge(left, right, on="key", how="right")

left

	key	lval
0	jamie	15
1	bill	22

right

	key	rval
0	jamie	4
1	bill	5
2	asher	8

merged

	key	lval	rval
0	jamie	15.0	4
1	bill	22.0	5
2	asher	NaN	8

Notice the NaN inserted into the record with key='asher', since the left table didn’t contain the key.

Matching column names
In this next example, the value columns have the same name: val. Notice what happens to the column names.

left = pd.DataFrame({"key": ["jamie", "bill"], "val": [15, 22]})
right = pd.DataFrame({"key": ["jamie", "bill", "asher"], "val": [4, 5, 8]})
merged = pd.merge(left, right, on="key", how="right")

left

	key	val
0	jamie	15
1	bill	22

right

	key	val
0	jamie	4
1	bill	5
2	asher	8

merged

	key	val_x	val_y
0	jamie	15.0	4
1	bill	22.0	5
2	asher	NaN	8

`.join()`

An SQL-like joiner, but this one takes advantage of indexes.

Give our dataframes indexes and distinctive columns names.

Details

left2 = left.set_index('key').copy()
right2 = right.set_index('key').copy()

left2

	val
key
jamie	15
bill	22

right2

	val
key
jamie	4
bill	5
asher	8

right2.join(left2, rsuffix='_y') # Defaults to 'left'

	val	val_y
key
jamie	4	15.0
bill	5	22.0
asher	8	NaN

right2.join(left2, rsuffix='_y', how='inner')

	val	val_y
key
jamie	4	15
bill	5	22

Summary

Use join if you have shared indexes
Use merge if you do not have shared indexes
Use concat to combine based on shared indexes or columns
Pay attention to resulting dataframe indexes and column names

Reshape with `.reshape()`

Changes the object’s shape

We illustrate creating pandas Series, extracting array of length 6, and reshaping to 3x2 array.

Create a series:

ser = pd.Series([1, 1, 2, 3, 5, 8])

Extract values:

vals = ser.values

vals

array([1, 1, 2, 3, 5, 8])

type(vals)

numpy.ndarray

vals.shape

(6,)

Reshaping a series:

reshaped_vals = vals.reshape((3, 2))

reshaped_vals

array([[1, 1],
       [2, 3],
       [5, 8]])

type(reshaped_vals)

numpy.ndarray

reshaped_vals.shape

(3, 2)

Including -1 as one of the dimensions tells numpy: infer this dimension from the data and the other dimensions.

Example: enforce 3 columns:

vals.reshape(-1,3)

array([[1, 1, 2],
       [3, 5, 8]])

Enforce 3 rows:

vals.reshape(3,-1)

array([[1, 1],
       [2, 3],
       [5, 8]])

Notice the shape of original array: (6,).

This is a vector with one dimension, and is different from two-dimensional (6,1) array.

Categoricals

Categorical data takes discrete values where computation on the values does not make sense.

Zip code is a typical example.

To include categoricals in models, often they must be converted to numeric form.

`get_dummies()`

Dummy code categorical data

Important parameters:

prefix : append prefix to column names (a good idea for later use)
drop_first: remove first level, as only k-1 variables needed to represent k levels

Details

cats = pd.DataFrame({'breed':['persian', 'persian', 'siamese', 'himalayan', 'burmese']})

cats

	breed
0	persian
1	persian
2	siamese
3	himalayan
4	burmese

dummy_cats = pd.get_dummies(cats.breed, prefix='breed')

dummy_cats

	breed_burmese	breed_himalayan	breed_persian	breed_siamese
0	0	0	1	0
1	0	0	1	0
2	0	0	0	1
3	0	1	0	0
4	1	0	0	0

pd.get_dummies(cats.breed, drop_first=True, prefix='breed')

	breed_himalayan	breed_persian	breed_siamese
0	0	1	0
1	0	1	0
2	0	0	1
3	1	0	0
4	0	0	0

Notice burmese was dropped (first level by alphabet) since it can be inferred.

Let’s try it on the iris dataset.

iris

	sepal_length	sepal_width	petal_length	petal_width	species	sepal_len_sq	sepal_len_wid_avg
0	5.1	3.5	1.4	0.2	setosa	26.01	4.30
1	4.9	3.0	1.4	0.2	setosa	24.01	3.95
2	4.7	3.2	1.3	0.2	setosa	22.09	3.95
3	4.6	3.1	1.5	0.2	setosa	21.16	3.85
4	5.0	3.6	1.4	0.2	setosa	25.00	4.30
...	...	...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	virginica	44.89	4.85
146	6.3	2.5	5.0	1.9	virginica	39.69	4.40
147	6.5	3.0	5.2	2.0	virginica	42.25	4.75
148	6.2	3.4	5.4	2.3	virginica	38.44	4.80
149	5.9	3.0	5.1	1.8	virginica	34.81	4.45

150 rows × 7 columns

Called get_dummies() by itself will handle all categoricals for you.

Look at what happened to the species column.

pd.get_dummies(iris)

	sepal_length	sepal_width	petal_length	petal_width	sepal_len_sq	sepal_len_wid_avg	species_setosa	species_versicolor	species_virginica
0	5.1	3.5	1.4	0.2	26.01	4.30	1	0	0
1	4.9	3.0	1.4	0.2	24.01	3.95	1	0	0
2	4.7	3.2	1.3	0.2	22.09	3.95	1	0	0
3	4.6	3.1	1.5	0.2	21.16	3.85	1	0	0
4	5.0	3.6	1.4	0.2	25.00	4.30	1	0	0
...	...	...	...	...	...	...	...	...	...
145	6.7	3.0	5.2	2.3	44.89	4.85	0	0	1
146	6.3	2.5	5.0	1.9	39.69	4.40	0	0	1
147	6.5	3.0	5.2	2.0	42.25	4.75	0	0	1
148	6.2	3.4	5.4	2.3	38.44	4.80	0	0	1
149	5.9	3.0	5.1	1.8	34.81	4.45	0	0	1

150 rows × 9 columns

You can call it one numeric columns, too.

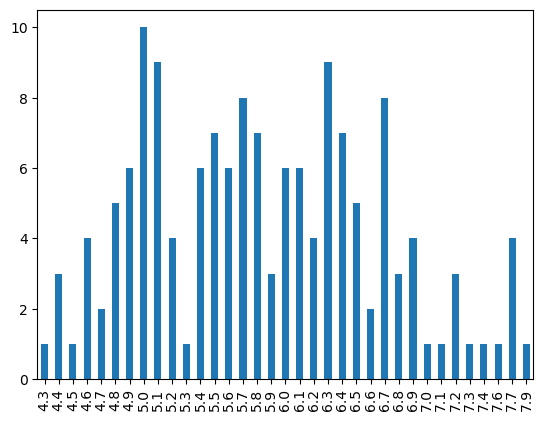
pd.get_dummies(iris.sepal_length).sum().plot.bar()

<Axes: >

Set Up

Apply Lambda Functions with .apply()

Aggregation

.groupby()

pd.pivot_table()

Stacking and Unstacking

.unstack()

.stack()

Combining DataFrames

pd.concat()

.merge()

.join()

Summary

Reshape with .reshape()

Categoricals

get_dummies()

Apply Lambda Functions with `.apply()`

`.groupby()`

`pd.pivot_table()`

`.unstack()`

`.stack()`

`pd.concat()`

`.merge()`

`.join()`

Reshape with `.reshape()`

`get_dummies()`